Procedural generation casual gaming dungeons

The post examines in detail the technique of generating random dungeons. The main generation algorithm, an example of which can view here used by game developers TinyKeep. Original post from the developer of was posted on reddit.
the Original description of the algorithm
1. First I set the right number of rooms – for example, 150. Of course, the figure is arbitrary, and the bigger it is, the more difficult the dungeon.
2. For each room I create a rectangle with random width and height within a specified radius. The radius is not of great importance, although it is reasonable to assume that it should be proportional to the number of rooms.
Instead of uniformly distributed random numbers (which gives a generator of Math.random in most languages), I use normal distribution Park-Miller. As a result, the probability of occurrence of small rooms is higher than the probability of the emergence of large. Why is it necessary, I'll explain later.
In addition I check that the ratio of length and width of the room is not too large. We don't need as perfect of a square room, and greatly elongated.
3. And here we have a random 150 rooms, located in a small space. Most of them bump on each other. Now we carry out the separation technology separation steering to divide the rectangles so that they do not overlap. As a result, they do not overlap but are close enough to each other.
4. Fill the spaces with cells of size 1x1. As a result, we obtained a square grid of rooms of various sizes.
5. And here starts the main fun. Determine which of the cells of the lattice are is there are any cells with width and height that exceeds the specified. Due to distribution of Park-Miller, we get a relatively small number of rooms, among which there are quite a lot of space. But the remaining cells, we also will be useful.
6. The next step is tying the rooms together. To do this, we build a graph that contains the centers of all the rooms with Delaunay triangulation. Now all the rooms are connected with each other non-intersecting lines.
7. Since we don't need all the rooms were connected with all, we build minimum spanning tree. The result is a graph, which can be guaranteed to reach any room.
8. The tree turns out to be a neat, but boring – no you closed moves. Therefore, we randomly added back approximately 15% of previously excluded edges in the graph. The result is a graph, where all rooms are guaranteed to be achievable, with a few closed passages.
9. To turn it into corridors, for each edge, draw a series of straight lines (G) running along the edges of the graph connecting the rooms. Here we useful those cells which remained unused (those not turned into rooms). All of the cells, superimposed on the G-lines become corridors. And because of the diversity in the size of cells the walls of the corridors are uneven, that is just good for dungeons.
And here is a sample output!
Caution — under the cut a lot
In a post on Gamasutra user A Adonaac took the trouble to describe some more details. In General, the algorithm looks as follows:

rooms
First you need to create a few rooms with a defined height and width, randomly located inside a given circle. The algorithm TKdev used a normal distribution to select the size of the rooms, and I think it's a good idea, you have more options with which to play. Different types of dungeons can be achieved by choosing different relations of height to width and the standard deviation.
One of the features you may need — getRandomPointInCircle:
the
function getRandomPointInCircle(radius)
local t = 2*math.pi*math.random()
local u = math.random()+math.random()
local r = nil
if u > 1 then r = 2-u else r = - u end
return the radius*r*math.cos(t), radius*r*math.sin(t)
end
Here read more here described her work. You can then obtain something like the following:

It is important to note that since you are dealing with a grid of tiles, you will need to place all of the room along one of the lattice. In the above GIF tiles have a size of 4 pixels, therefore all the positions and sizes of rooms should be a multiple of 4-m. To do this, I wrapped the assignment of positions and height with the width in functions to round numbers up to the size of the tile:
the
function roundm(n, m) return math.floor(((n + m - 1)/m))*m end
- Now you can change the return value of getRandomPointInCircle:
getRandomPointInCircle function(radius)
...
roundm return(radius*r*math.cos(t), tile_size),
roundm(radius*r*math.sin(t), tile_size)
end
Shared room
Let's move on to the division. We got a lot of overlapping each other rooms that need to be divided. TKdev mentions the separation steering technology, but it seems more simple use of physics engine. After the creation of a set of rooms, you just need to assign the physical body of each room, to start the simulation and wait until things calm down. In the GIF shows you an example of work simulation.

The physical body is not tied to our bars, but, assigning of positions, we wrap them in calls roundm, resulting in rooms, not overlapping each other and mounted on the grid. In the GIF illustrates this process. The blue contours represent the physical body. Between them and the real positions of the rooms there is a small discrepancy due to the constant rounding.

One of the problems that can occur at the same time, can meet you if you are specifically trying to get the room mainly along one of the axes. Consider for example the game that I'm working on:

Since battles take place horizontally, I need the room was stretched in width, not height. The problem is how the physics engine will allow the collision of two rooms between them.

The picture we get of the dungeon, stretched vertically, which is not very convenient. To remedy the situation, you can initially set the arrangement so they will not appear inside the circle, and inside thin strips. As a result, we get the desired ratio of the height and width of the dungeon.

For a random distribution of rooms in the strip will change the function of getRandomPointInCircle to put the points in the ellipse and not the circle (represented in the GIF I use values ellipse_width = 400 and ellipse_height = 20):
the
function getRandomPointInEllipse(ellipse_width, ellipse_height)
local t = 2*math.pi*math.random()
local u = math.random()+math.random()
local r = nil
if u > 1 then r = 2-u else r = - u end
return roundm(ellipse_width*r*math.cos(t)/2, tile_size),
roundm(ellipse_height*r*math.sin(t)/2, tile_size)
end
Main room
In the next step we define the room, which will be the main. The algorithm TKdev it's simple – choose those rooms, the height and width which exceed the specified values. On the next GIF I used a limit of 1.25*mean – that is, if width_mean and height_mean equal to 24, then become the main room with a height and width greater than 30.
Delaunay Triangulation and graph
Now we take the centers of the selected rooms and fed the data into the procedure. You can write yourself or get ready – I was lucky and I found ready for authorship Yonaba. She takes a point and outputs the triangles

Getting the triangles to construct the graph. Hint: it is convenient to assign the rooms a unique id, and to work with them and not copy the actual objects in the rooms.
Minimum spanning tree
Then create a minimum spanning tree based graph. It ensures that all rooms are in principle achievable, and in addition, each room is not connected directly with all the others.
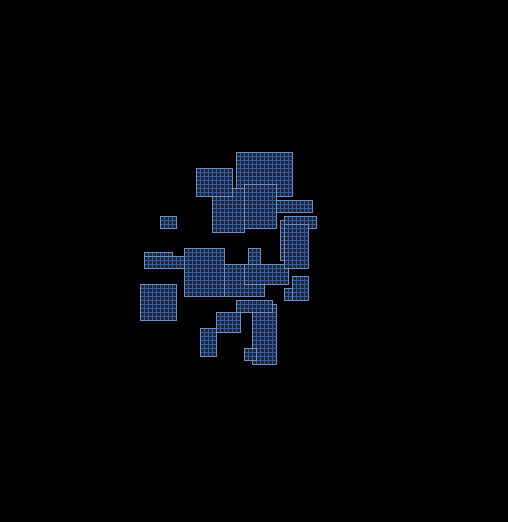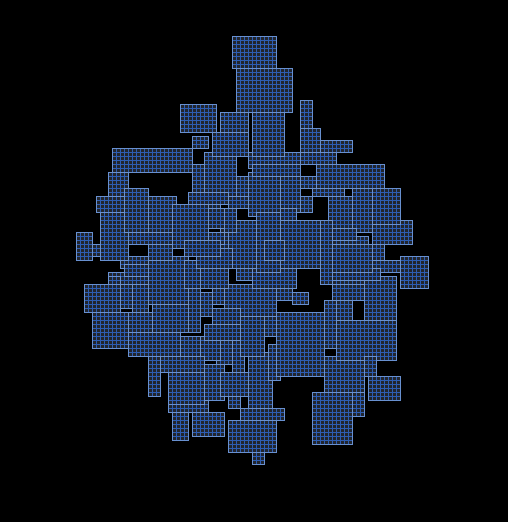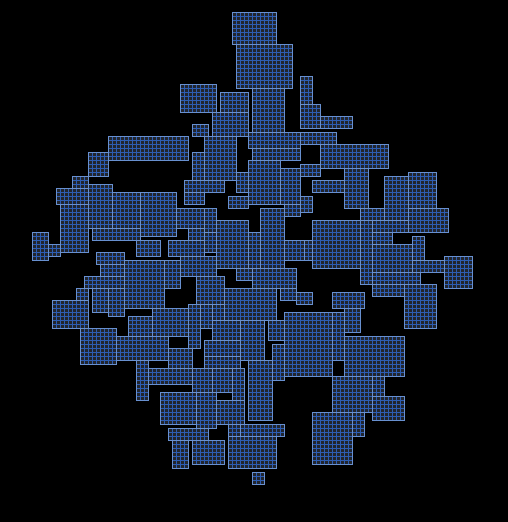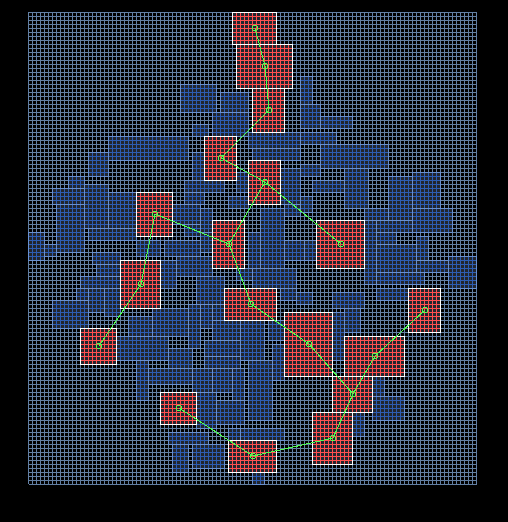
We don't need as too many corridors and rooms, which are not available. But it will be boring and the dungeon in which only one right way – so we will return some edges from the Delaunay graph.

This will add more ways and generate a little enclosed. TKdev recommends to return 15% of the edges, but I personally think it is more convenient to return 8-10%.
Corridors
To add corridors, we pass all nodes of the graph and create a line connecting it with all neighboring nodes. If the node is about the same horizontally, creating a horizontal line. If vertical is vertical. If the nodes are not located on the same horizontal or vertical, we create two lines forming an l-shaped form.
I implemented this check by finding the midpoint between the positions of two nodes, and checking whether the coordinate of this point on the room level (horizontal or vertical). If they are on the level, I'll take one line. If not – two, from room to point and point to another room.
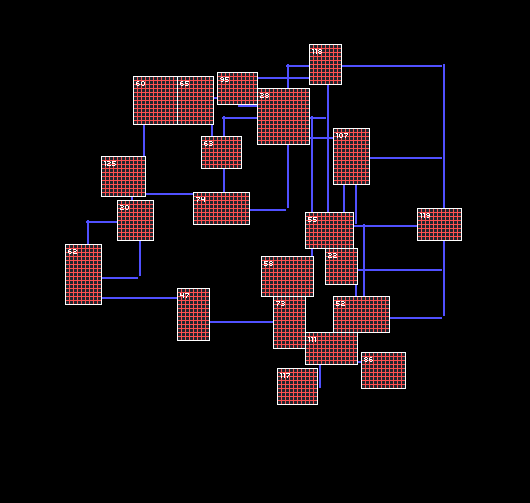
In this picture you can see examples of all cases. The nodes 62 and 47 are connected by a horizontal line nodes 60 and 125 to the vertical, the nodes 118 and 119 is l-shaped. I note that in addition to the picture lines, I create 2 extra on each side of the drawn line, at a distance tile_size – because I need the corridors with a minimum width of 3 cells.
After that we check which of the rooms that are not primary, intersect constructed lines. These rooms are added to our structure and become the basis of a system of corridors.
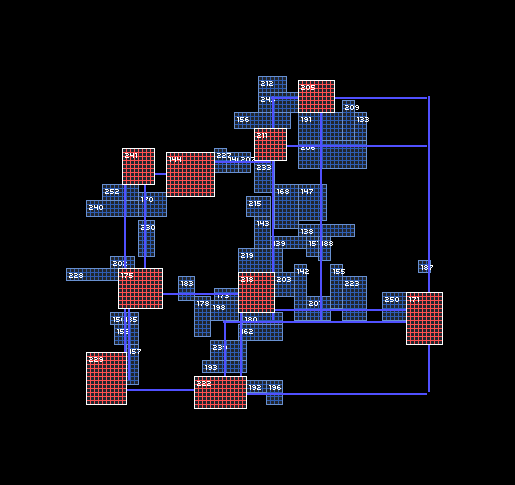
Depending on the uniformity and maximum size, as a result, you can get very different dungeons. If you want to obtain more uniform corridors, you need to limit the standard deviation and introduce more checks on size of rooms and the ratio of their height and width.
Finally, we add to the lines of cells of 1x1 size, offsetting the missing parts. It is here and can be useful to previously added additional lines to the corridors was not too narrow.

That's all, folks!

As a result I get a data structure that has:
the
-
the
- list rooms (each of which is a structure with a unique id, position x/y and height/width) the
- graph, where each node indicates the id of the room, and the edges contain the distance between the rooms in the cells the
- 2D grid in which each cell can be empty, point to a main room, specify the room belonging to the system of corridors, or on the cell of the narrow corridor
These three structures can be used to represent any required data set. On their basis it is already possible to work with location of doors, enemies, items, etc.

Комментарии
Отправить комментарий